Cellular Automaton

1

October 11, 2012 by Nakul

Author: Nischal Rao

A cellular automaton is a collection of cells on a grid of specified shape that evolves through a number of discrete time steps according to a set of rules based on the states of neighboring cells.
The grid can be in any finite number of dimensions. Each cell in the grid can be in a finite number of states. For each cell, a set of cells called its neighborhood (usually including the cell itself) is defined relative to the specified cell. The pre-defined rules are then applied iteratively for as many time steps as desired on the cells to find the next generations. The rules applicable for a cell are generally the same in a grid.
The concept was originally discovered in the 1940s by Stanislaw Ulam and John von Neumann while they were working at Los Alamos National Laboratory. It was studied throughout the 1950s and 1960s, but it was not until the 1970s that interest in the subject expanded beyond academia. In the 1980s, Stephen Wolfram engaged in a systematic study of one dimensional cellular automaton, or what he calls elementary cellular automata, claiming that it had application in various fields of science. He classified the rules, and in order of complexity, the classes are as follows:
Class 1: Randomness in initial pattern disappears and they evolve quickly into a stable homogenous state.
Class 2: Randomness in initial pattern may filter out, but some remains, they evolve quickly into stable or oscillating structures.
Class 3: Stable structures that appear are quickly destroyed by surrounding noise; they evolve in a pseudo-random or chaotic manner.
Class 4: The eventual outcome is often class 2 type stable or oscillating structures, but to reach it may take a large number of steps. Initial structures interact in complex ways.

Cellular automaton can be in a variety of shapes and varieties. One of the most fundamental properties of a cellular automaton is the type of grid on which it is computed. The simplest such “grid” is a one-dimensional line. In two dimensions, square, triangular, and hexagonal grids may be considered. Cellular automata may also be constructed on Cartesian grids in arbitrary numbers of dimensions.
In addition to the grid on which a cellular automaton exists and the colours/values its cells may assume, the neighborhood over which cells affect one another must also be specified. The simplest choice is “nearest neighbors ” in which only cells directly adjacent to a given cell may be affected at each time step. Two common neighborhoods in the case of a two-dimensional cellular automaton on a square grid are the so-called Moore neighborhood (a square neighborhood) and the von Neumann neighborhood (a diamond-shaped neighborhood).
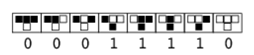
The simplest automaton is a one-dimensional cellular automaton. Rule 30 which is an one-dimensional cellular automaton is as shown in the figure below:

Rule 30 was originally suggested as a possible Block cipher for use in cryptography. Two dimensional cellular automata are used for random number generation.
A reversible cellular automaton is the one that has got exactly one past configuration ( also called pre-image) for every current configuration. There are algorithms existing which determine if a particular cellular automata rule is reversible or not for one- dimensional cellular automaton, however the same do not exist for two or higher dimensional cellular automata rules. Reversible cellular automata find applications in areas such as gas and fluid dynamics. Non-reversible cellular automata are used in cryptography.
Cellular automata have been proposed for public key cryptography. The one-way function is the evolution of a finite cellular automaton whose inverse is not easy to find. Given the rule, anyone can easily calculate future states, but it is very difficult to calculate previous states. However, the designer of the rule can create it in such a way as to be able to easily invert it. Therefore, it is like a trapdoor function, and can be used as a public-key cryptosystem.